# 卷积神经网络
学习内容基于:Pytorch 框架与经典卷积神经网络与实战
# CNN 卷积神经网络算法原理
# 全连接神经网络
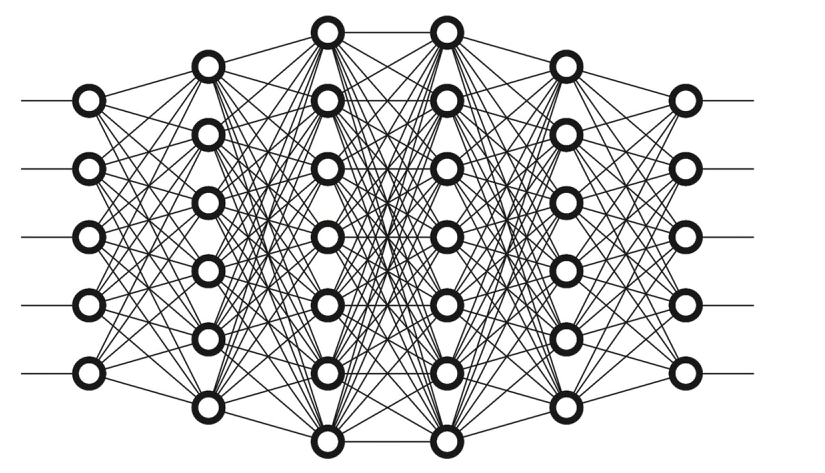
输入层是我们输入的数据,这里看到的第一列节点并不是输入层,中间为隐藏层。
输入层就像 X(自变量),模型或者说这些网络就是 F(函数),我们得到的输出就是 Y(因变量)。
# 为什么要使用激活函数
在神经网络中使用激活函数的根本原因是引入非线性,从而使模型能够拟合和表达复杂的函数关系。如果没有激活函数,神经网络无论堆叠多少层,本质上都是一个线性模型,能力极其有限。多层线性变换的叠加依然是线性变换,最终的模型只能拟合直线 / 平面,完全无法处理复杂的数据模式
# Sigmoid 激活函数
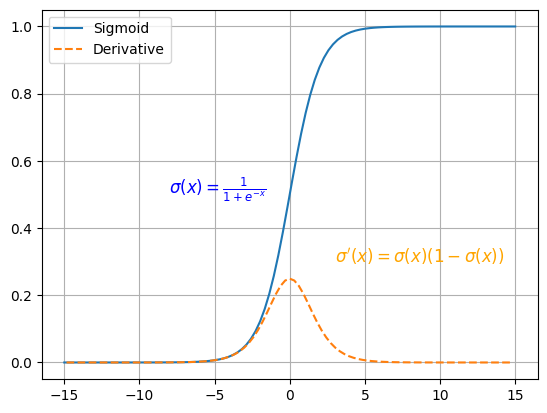
优点:简单、非常适用分类任务。
缺点:反向传播训练时有梯度消失的问题;输出值区间为 (0,1),关于 0 不对称;梯度更新在不同方向走得太远,使得优化难度增大,训练耗时。
# Tanh 激活函数
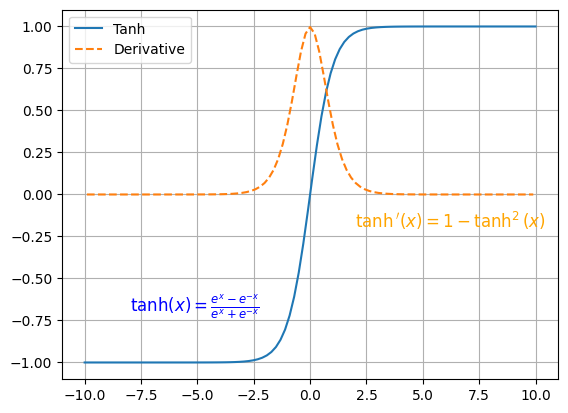
优点:解决了 Sigmoid 函数输出值非 0 对称的问题,训练比 Sigmoid 函数快,更容易收敛
缺点:反向传播训练时有梯度消失的问题,Tanh 函数和 Sigmoid 函数非常相似。
# ReLU 激活函数
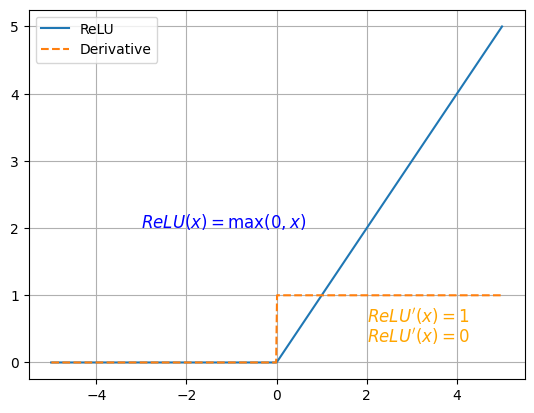
优点:解决了梯度消失的问题;计算更为简单,没有 Sigmoid 函数和 Tanh 函数的指数运算
缺点:训练时可能出现神经元死亡
# Leaky ReLU 激活函数
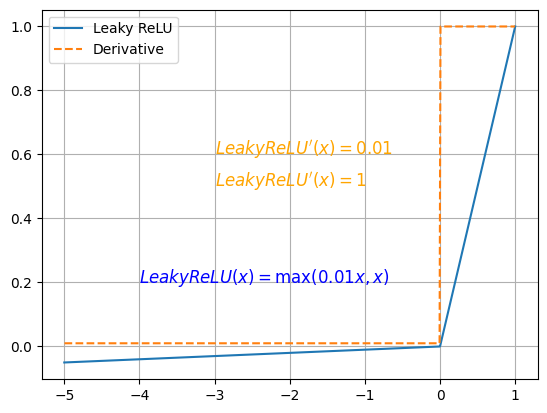
优点:解决了 ReLU 的神经元死亡问题
缺点:无法为正负输入值提供一致的关系预测 (不同区间函数不同)
# 前向传播
前向传播是神经网络中数据从输入层依次流向输出层的过程,它的核心目标是根据当前的模型参数(权重和偏置)计算出预测结果。
前向传播就是 “把输入数据依次喂给每一层,经过线性计算 + 激活函数,逐层输出,最后得到预测值” 的过程。
# 损失函数
# 均方误差
 |
 |
|---|
前面有可能有出现 1/2,那只是为了方便求导,都是均方误差。
# 梯度下降法
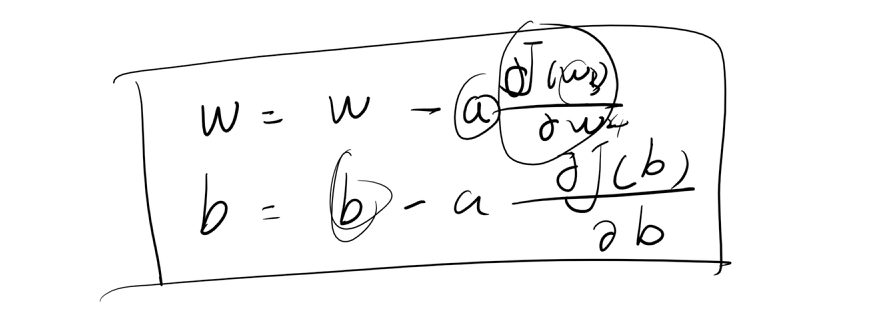
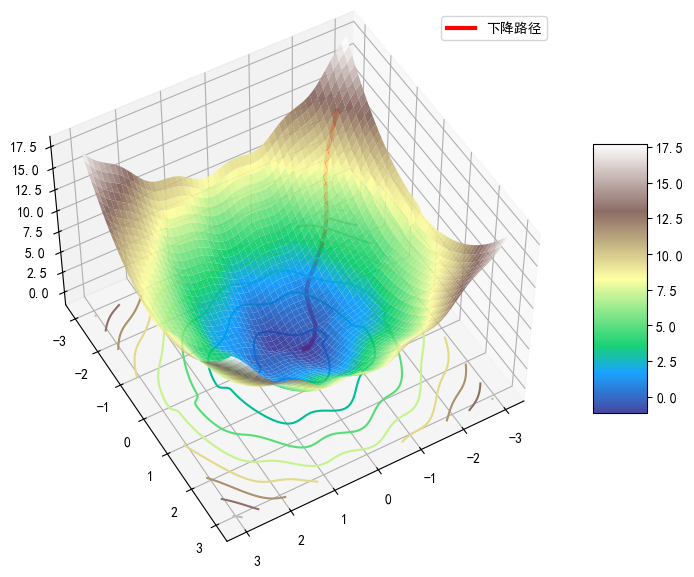
# 全连接神经网络在图片中存在的问题
# 1. 参数量巨大
- 全连接层的每一个神经元都与上一层的所有神经元相连。
- 对于图片来说,输入通常是高维的,例如一张 224×224 的 RGB 图片就是 224×224×3 = 150,528 个输入特征。
- 假设第一层有 1000 个神经元,那么权重数量就是 150,528 × 1000 ≈ 1.5 亿个参数!
- 问题:参数太多 → 容易过拟合 → 训练时间长 → 需要大量显存。
# 2. 忽略空间结构
- 图片是二维或三维(RGB)的网格数据,有局部空间相关性(邻近像素往往相关)。
- 全连接层把图片 “拉平” 成一维向量,然后再进行矩阵乘法。
- 问题:丢失了图片的空间信息(如边缘、纹理、形状),无法有效捕捉局部特征。
# 3. 缺乏平移不变性
- 图像中物体的位置可能变化。
- 全连接网络对输入的每个位置都固定,物体稍微移动,输出可能完全不同。
- 问题:无法自动识别图像中的平移或局部位移,泛化能力差。
# 4. 计算效率低
- 全连接层计算复杂度高(矩阵乘法量大)。
- 对高分辨率图像,训练和推理速度都很慢。
- 对比卷积神经网络(CNN),后者通过卷积核共享权重大幅减少计算量。
# 5. 不适合捕捉层次特征
- 图片的特征是有层次结构的:边缘 → 纹理 → 形状 → 对象。
- 全连接层一次性处理所有像素,无法自然学习层次特征。
- CNN 则通过卷积和池化层逐步抽象特征,更符合视觉认知规律。
# 卷积、步幅、填充、池化
这部分请看:
https://735690757.github.io/python/pytorch
# 经过卷积后特征图大小
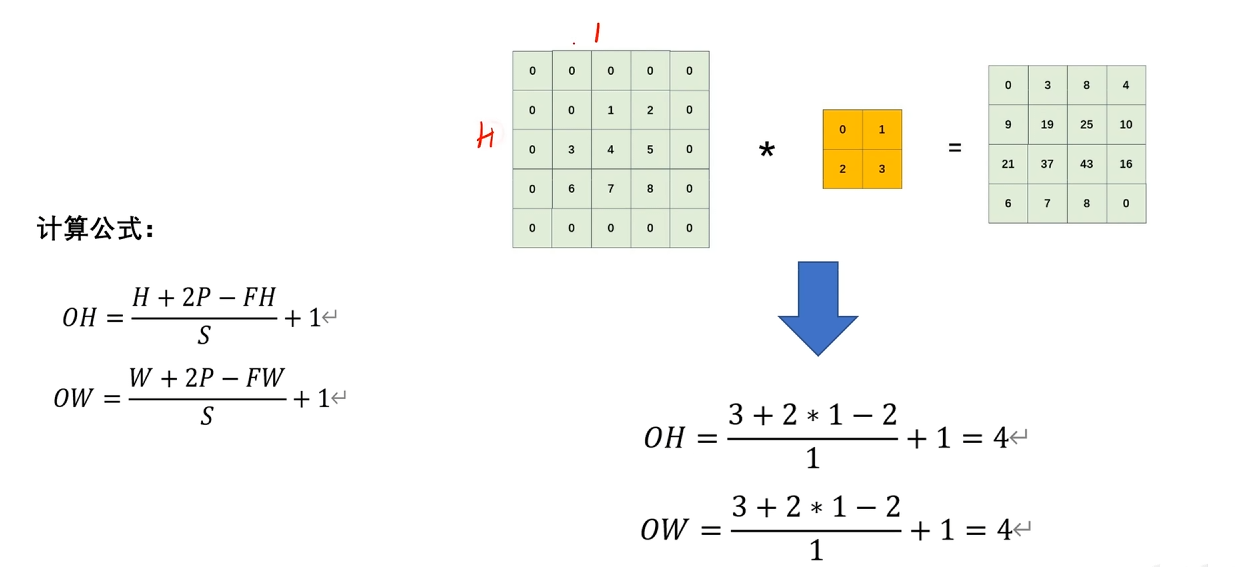
FH:卷积核(filter)的高度(Filter Height)
FW:卷积核的宽度(Filter Width)
C_in:输入通道数(Input Channels)
C_out:输出通道数(Output Channels)
S:步幅(Stride)
P:填充(Padding)
如果算出来是小数,一般是向下取整。
# LeNet 与 AlexNet 原理
# LeNet-5 诞生背景
简单来说,LeNet-5 的诞生背景是为了解决手写数字识别这一实际应用问题,它是世界上首个成功商用的卷积神经网络,奠定了现代深度学习的基础。
# LeNet-5 网络结构
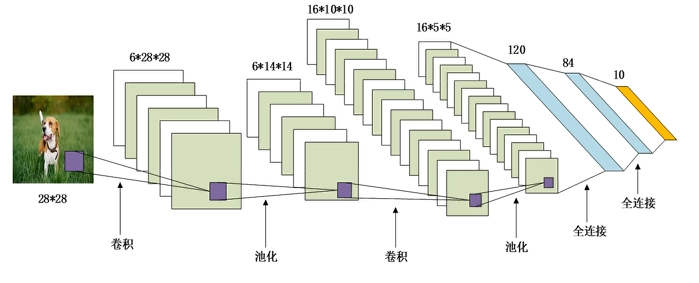
- 输入 1 * 28 * 28
- 5 * 5 卷积(6),填充 2
- 2 * 2 平均池化层,步幅 2
- 5 * 5 卷积(16),填充 0
- 2 * 2 平均池化层,步幅 2
- 全连接(120)
- 全连接(84)
- 全连接(10)
再强调一下:

这个计算公式非常重要。
# AlexNet 诞生背景
在算力达到临界点、大数据已经就位的环境下,一个古老但曾被忽视的算法(深度学习 / 卷积神经网络)迎来了证明自己的最佳时机。AlexNet 不仅仅是一个优秀的模型,它更是一个时代的开创者,是人工智能发展史上的一个关键转折点。
# AlexNet 网络结构
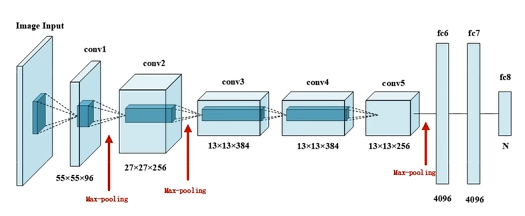
5 层卷积,3 层全连接,共 8 层,激活函数使用 ReLU。
- 输入 3 * 227 * 227(?这个可能有问题)
- 11 * 11 卷积(96),步幅 4,ReLU
- 3 * 3 最大池化,步幅 2
- 5 * 5 卷积(256),填充 2,ReLU
- 3 * 3 最大池化,步幅 2
- 3 * 3 卷积(384),填充 1,ReLU
- 3 * 3 卷积(384),填充 1,ReLU
- 3 * 3 卷积(256),填充 1,ReLU
- 3 * 3 最大池化,步幅 2
- 全连接(4096)
- 全连接(4096)
- 全连接(10)
这里在全连接层有很多的参数,参数太多容易过拟合,我们引入了 Dropout 操作。
# 图像增强 - 水平翻转
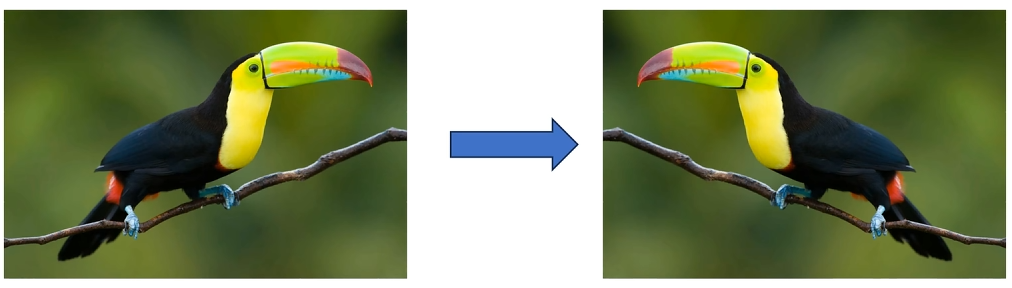
# 图像增强 - 随机裁剪
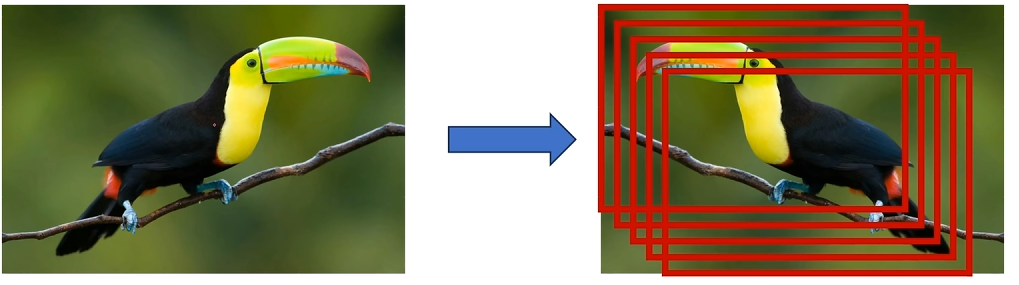
# 图像增强 - PCA

| 方面 | 描述 |
|---|---|
| 核心思想 | 利用 PCA 找到图像颜色的主要变化方向,并沿这些方向添加随机扰动来模拟光照变化。 |
| 目的 | 增强模型对颜色和光照变化的鲁棒性,是一种高效的数据增强手段。 |
| 优点 | 变化方式基于图像自身的统计特性,生成的图像颜色变化自然、合理。 |
| 缺点 | 计算成本相对较高(需要对每张图或每批图做 PCA)。 |
| 遗产 | 是 AlexNet 的一个创新点,启发了对颜色增强的重视,但已被更简单高效的方法所取代。 |
# LRN 正则化
这是一个针对通道间的计算

尽管 LRN 是 AlexNet 的一个关键创新,但在后续更深、更先进的网络(如 VGG、ResNet)中,它几乎被完全弃用了。主要原因如下:
- 效果有限且不稳定:后续研究发现,LRN 带来的性能提升非常微弱,甚至有时不稳定。其正则化效果远不如 Dropout 和 Batch Normalization(BN) 那样显著和可靠。
- 被更好的技术取代:
- Dropout:通过随机断开神经元连接来防止过拟合,更为直接有效。
- Batch Normalization(批归一化):这是革命性的技术。BN 对整个 Batch 的每个通道进行归一化(均值为 0,方差为 1),极大地改善了梯度流动,加速了训练,同时本身也具有轻微的正则化效果。BN 的效果远超 LRN,并且已经成为现代深度网络的标准组件。
- 增加计算开销和超参数:LRN 引入了额外的计算量,并且
k, α, β, n这些超参数需要调优,增加了模型设计的复杂性。
# 重叠池化
与 LRN 类似,重叠池化在现代深度学习架构中也已经不常用了。
- 计算成本更高:由于存在重叠,为了得到相同尺寸的输出特征图,重叠池化需要进行更多次池化操作。例如,将
5x5降采样到2x2,非重叠池化 (2x2, stride=2) 需要 4 次操作,而重叠池化 (3x3, stride=2) 也需要 4 次操作,但每次操作的窗口更大,计算量稍高。 - 被更有效的技术取代:如今,防止过拟合和提升性能的重任更多地由 Batch Normalization、更深的网络结构(如 ResNet 的残差连接)、更先进的优化器 和 Dropout 等方法来承担。
- 设计趋势变化:现代网络有时甚至会完全摒弃池化层,转而使用步长大于 1 的卷积(Strided Convolution) 来同时实现特征提取和降采样,这被认为能提供更大的模型容量和灵活性。
# LeNet 实战
# 模型
class LeNet(nn.Module): | |
def __init__(self, *args, **kwargs) -> None: | |
super().__init__(*args, **kwargs) | |
self.block = nn.Sequential( | |
nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5, stride=1, padding=2), | |
nn.Sigmoid(), | |
nn.AvgPool2d(kernel_size=2, stride=2), | |
nn.Conv2d(in_channels=6, out_channels=16, kernel_size=5, stride=1, padding=0), | |
nn.Sigmoid(), | |
nn.AvgPool2d(kernel_size=2, stride=2), | |
nn.Flatten(), | |
nn.Linear(in_features=400, out_features=120), | |
nn.Sigmoid(), | |
nn.Linear(in_features=120, out_features=84), | |
nn.Sigmoid(), | |
nn.Linear(in_features=84, out_features=10) | |
) | |
def forward(self, x): | |
return self.block(x) |
# 设备、实例化与 summary
device = torch.device("cuda" if torch.cuda.is_available() else "cpu") | |
net = LeNet().to(device) | |
summary(net, (1, 28, 28)) |
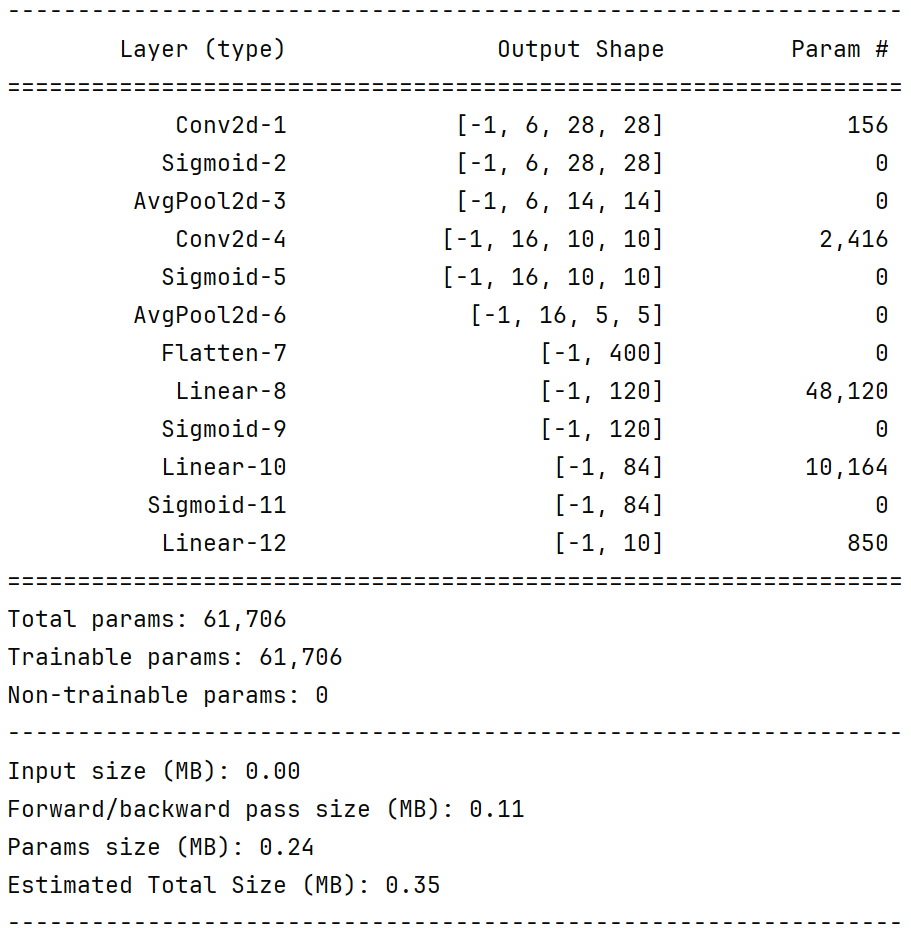
这里的 -1 代表的是 批量大小,更具体地说:-1 是一个占位符,表示这个维度的大小是由其他维度推断出来的,而不是一个固定值。
批量大小:在深度学习训练中,数据通常是按批次(batch)输入的。比如,你可能会一次输入 32 张图片、64 张图片等。这个数量就是批量大小。
为什么是 -1?:PyTorch 模型在设计时,其核心计算逻辑不依赖于具体的批量大小。为了增加灵活性,在定义模型的前向传播时,我们通常将输入张量的第一个维度设为批量大小。当打印模型摘要时,库(如 torchsummary)无法预先知道你会用多大的批量大小来训练,所以它使用 -1 来代表 “任何尺寸”。
动态推断:在实际运行中,这个 -1 会被你输入数据的真实批量大小所替代。
例如,如果你用一批 32 张图片输入到模型,那么 [-1, 1, 32, 32] 就会变成 [32, 1, 32, 32]。
如果你用 128 张图片,它就会变成 [128, 1, 32, 32]。
# 加载 FashionMNIST
from torchvision.datasets import FashionMNIST | |
from torchvision.transforms import transforms | |
import numpy as np |
transform = transforms.Compose([ | |
transforms.Resize((28, 28)), | |
transforms.ToTensor(), | |
transforms.Normalize((0.5,), (0.5,)) | |
]) | |
train_data = FashionMNIST(root="./data/FashionMNIST", train=True, download=True, transform=transform) | |
test_data = FashionMNIST(root="./data/FashionMNIST", train=False, download=True, transform=transform) |
from torch.utils.data import DataLoader | |
train_dataLoader = DataLoader(train_data, batch_size=64, shuffle=True) | |
test_dataLoader = DataLoader(test_data, batch_size=64, shuffle=False) |
# 展示
import matplotlib.pyplot as plt | |
for setp, (features, label) in enumerate(train_dataLoader): | |
if setp == 0: | |
x = features.squeeze().numpy() | |
y = label.numpy() | |
break | |
plt.figure(figsize=(12, 5)) | |
for ii in np.arange(len(y)): | |
plt.subplot(4, 16, ii+1) | |
plt.imshow(x[ii,:,:], cmap=plt.cm.gray) | |
plt.title(y[ii]) | |
plt.axis("off") | |
plt.show() |
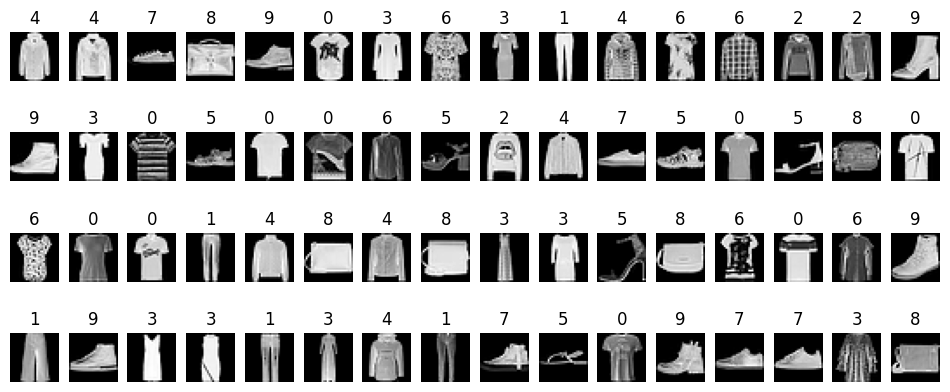
# 训练、验证(此处为最佳实践)
from torch.optim.lr_scheduler import CosineAnnealingLR | |
from tqdm import tqdm | |
import copy | |
import time | |
import pandas as pd | |
def train_model_process(model, train_dataloader, val_dataloader, num_epochs): | |
device = torch.device("cuda" if torch.cuda.is_available() else "cpu") | |
optimizer = torch.optim.Adam(model.parameters(), lr=0.001) | |
scheduler = CosineAnnealingLR( | |
optimizer, | |
T_max=num_epochs, | |
eta_min=1e-6 | |
) | |
criterion = nn.CrossEntropyLoss().to(device) | |
model = model.to(device) | |
best_model_wts = copy.deepcopy(model.state_dict()) | |
best_acc = 0.0 | |
train_loss_all = [] | |
val_loss_all = [] | |
train_acc_all = [] | |
val_acc_all = [] | |
learning_rates = [] | |
since = time.time() | |
for epoch in range(num_epochs): | |
print("Epoch {}/{}".format(epoch, num_epochs - 1)) | |
print("-" * 10) | |
current_lr = optimizer.param_groups[0]['lr'] | |
learning_rates.append(current_lr) | |
print(f"当前学习率: {current_lr:.6f}") | |
train_loss = 0.0 | |
train_corrects = 0 | |
val_loss = 0.0 | |
val_corrects = 0 | |
train_num = 0 | |
val_num = 0 | |
for step, (b_x, b_y) in tqdm(enumerate(train_dataloader), desc=f"总步骤:{len(train_dataloader)}", | |
leave=False, unit="step", total=len(train_dataloader), | |
bar_format="{desc}: |{bar:30}| {percentage:3.0f}% 唱跳Rap🏀,Music~", | |
ascii="🏀🥰🥰😘"): | |
b_x = b_x.to(device) | |
b_y = b_y.to(device) | |
model.train() | |
output = model(b_x) | |
pre_lab = torch.argmax(output, dim=1) | |
loss = criterion(output, b_y) | |
optimizer.zero_grad() | |
loss.backward() | |
optimizer.step() | |
train_loss += loss.item() * b_x.size(0) | |
# 如果预测正确,则准确度 train_corrects 加 1 | |
train_corrects += torch.sum(pre_lab == b_y.data) | |
train_num += b_x.size(0) | |
for step, (b_x, b_y) in enumerate(val_dataloader): | |
b_x = b_x.to(device) | |
b_y = b_y.to(device) | |
model.eval() | |
output = model(b_x) | |
pre_lab = torch.argmax(output, dim=1) | |
loss = criterion(output, b_y) | |
val_loss += loss.item() * b_x.size(0) | |
val_corrects += torch.sum(pre_lab == b_y.data) | |
val_num += b_x.size(0) | |
train_loss_all.append(train_loss / train_num) | |
train_acc_all.append(train_corrects.double().item() / train_num) | |
val_loss_all.append(val_loss / val_num) | |
val_acc_all.append(val_corrects.double().item() / val_num) | |
print("{} train loss:{:.4f} train acc: {:.4f}".format(epoch, train_loss_all[-1], train_acc_all[-1])) | |
print("{} val loss:{:.4f} val acc: {:.4f}".format(epoch, val_loss_all[-1], val_acc_all[-1])) | |
if val_acc_all[-1] > best_acc: | |
best_acc = val_acc_all[-1] | |
best_model_wts = copy.deepcopy(model.state_dict()) | |
time_use = time.time() - since | |
print("训练和验证耗费的时间{:.0f}m{:.0f}s".format(time_use // 60, time_use % 60)) | |
scheduler.step() | |
model.load_state_dict(best_model_wts) | |
torch.save(best_model_wts, "models/best_model.pth") | |
train_process = pd.DataFrame(data={"epoch": range(num_epochs), | |
"train_loss_all": train_loss_all, | |
"val_loss_all": val_loss_all, | |
"train_acc_all": train_acc_all, | |
"val_acc_all": val_acc_all, | |
"learn_rates": learning_rates}) | |
return train_process |
def matplot_acc_loss(train_process): | |
# 显示每一次迭代后的训练集和验证集的损失函数和准确率 | |
plt.figure(figsize=(12, 4)) | |
plt.subplot(1, 3, 1) | |
plt.plot(train_process['epoch'], train_process.train_loss_all, "ro-", label="Train loss") | |
plt.plot(train_process['epoch'], train_process.val_loss_all, "bs-", label="Val loss") | |
plt.legend() | |
plt.xlabel("epoch") | |
plt.ylabel("Loss") | |
plt.subplot(1, 3, 2) | |
plt.plot(train_process['epoch'], train_process.train_acc_all, "ro-", label="Train acc") | |
plt.plot(train_process['epoch'], train_process.val_acc_all, "bs-", label="Val acc") | |
plt.xlabel("epoch") | |
plt.ylabel("acc") | |
plt.legend() | |
plt.subplot(1, 3, 3) | |
plt.plot(train_process['epoch'], train_process.learn_rates, "go-", label="Learn rates") | |
plt.xlabel("epoch") | |
plt.ylabel("Learn rates") | |
plt.legend() | |
plt.tight_layout() | |
plt.show() |
# 这里是优化后的版本
from torch.optim import lr_scheduler | |
import copy | |
import time | |
import pandas as pd | |
def train_model_process(model, train_dataloader, val_dataloader, num_epochs): | |
device = torch.device("cuda" if torch.cuda.is_available() else "cpu") | |
if not os.path.exists("models"): | |
os.mkdir("models") | |
optimizer = torch.optim.AdamW(model.parameters(), lr=3e-3, weight_decay=0.05) | |
scheduler = lr_scheduler.SequentialLR( | |
optimizer, | |
schedulers=[ | |
lr_scheduler.LinearLR(optimizer, start_factor=0.1, total_iters=15), | |
lr_scheduler.CosineAnnealingLR(optimizer, T_max=num_epochs-15, eta_min=1e-6) | |
], | |
milestones=[15] | |
) | |
criterion = nn.CrossEntropyLoss(label_smoothing=0.1).to(device) | |
model = model.to(device) | |
best_model_wts = copy.deepcopy(model.state_dict()) | |
best_acc = 0.0 | |
train_loss_all = [] | |
val_loss_all = [] | |
train_acc_all = [] | |
val_acc_all = [] | |
learning_rates = [] | |
since = time.time() | |
for epoch in range(num_epochs): | |
print("Epoch {}/{}".format(epoch, num_epochs - 1)) | |
print("-" * 10) | |
current_lr = optimizer.param_groups[0]['lr'] | |
learning_rates.append(current_lr) | |
print(f"当前学习率: {current_lr:.6f}") | |
train_loss = 0.0 | |
train_corrects = 0 | |
val_loss = 0.0 | |
val_corrects = 0 | |
train_num = 0 | |
val_num = 0 | |
for step, (b_x, b_y) in tqdm(enumerate(train_dataloader), desc=f"总步骤:{len(train_dataloader)}", | |
leave=False, unit="step", total=len(train_dataloader), | |
bar_format="{desc}: |{bar:30}| {percentage:3.0f}% 我在努力训练,唱跳Rap🏀,Music~", | |
ascii="🏀🥰🥰😘"): | |
b_x = b_x.to(device) | |
b_y = b_y.to(device) | |
model.train() | |
output = model(b_x) | |
pre_lab = torch.argmax(output, dim=1) | |
loss = criterion(output, b_y) | |
optimizer.zero_grad() | |
loss.backward() | |
optimizer.step() | |
train_loss += loss.item() * b_x.size(0) | |
# 如果预测正确,则准确度 train_corrects 加 1 | |
train_corrects += torch.sum(pre_lab == b_y.data) | |
train_num += b_x.size(0) | |
for step, (b_x, b_y) in tqdm(enumerate(val_dataloader), desc=f"总步骤:{len(val_dataloader)}", | |
leave=False, unit="step", total=len(val_dataloader), | |
bar_format="{desc}: |{bar:30}| {percentage:3.0f}% 该我上场表演了,唱跳Rap🏀,Music~", | |
ascii="🏀🥰🥰😘"): | |
b_x = b_x.to(device) | |
b_y = b_y.to(device) | |
model.eval() | |
output = model(b_x) | |
pre_lab = torch.argmax(output, dim=1) | |
loss = criterion(output, b_y) | |
val_loss += loss.item() * b_x.size(0) | |
val_corrects += torch.sum(pre_lab == b_y.data) | |
val_num += b_x.size(0) | |
train_loss_all.append(train_loss / train_num) | |
train_acc_all.append(train_corrects.double().item() / train_num) | |
val_loss_all.append(val_loss / val_num) | |
val_acc_all.append(val_corrects.double().item() / val_num) | |
print("{} train loss:{:.4f} train acc: {:.4f}".format(epoch, train_loss_all[-1], train_acc_all[-1])) | |
print("{} val loss:{:.4f} val acc: {:.4f}".format(epoch, val_loss_all[-1], val_acc_all[-1])) | |
if val_acc_all[-1] > best_acc: | |
best_acc = val_acc_all[-1] | |
best_model_wts = copy.deepcopy(model.state_dict()) | |
checkpoint = { | |
'epoch': epoch, | |
'model_state_dict': model.state_dict(), | |
'optimizer_state_dict': optimizer.state_dict(), | |
'scheduler_state_dict': scheduler.state_dict(), | |
'best_acc': best_acc, | |
} | |
torch.save(checkpoint, "models/best_checkpoint.pth") | |
time_use = time.time() - since | |
print("训练和验证耗费的时间{:.0f}m{:.0f}s".format(time_use // 60, time_use % 60)) | |
scheduler.step() | |
model.load_state_dict(best_model_wts) | |
torch.save(best_model_wts, "models/theBest.pth") | |
train_process = pd.DataFrame(data={"epoch": range(num_epochs), | |
"train_loss_all": train_loss_all, | |
"val_loss_all": val_loss_all, | |
"train_acc_all": train_acc_all, | |
"val_acc_all": val_acc_all, | |
"learn_rates": learning_rates}) | |
return train_process |
这里是学习率使用 0.01,可以得到更好的效果,学习率为 0.001 在图像上更美观。
# 测试(此处为最佳实践)
def test_model_process(model, test_dataloader): | |
device = "cuda" if torch.cuda.is_available() else 'cpu' | |
model = model.to(device) | |
test_corrects = 0.0 | |
test_num = 0 | |
with torch.no_grad(): | |
for test_data_x, test_data_y in test_dataloader: | |
test_data_x = test_data_x.to(device) | |
test_data_y = test_data_y.to(device) | |
model.eval() | |
output= model(test_data_x) | |
pre_lab = torch.argmax(output, dim=1) | |
test_corrects += torch.sum(pre_lab == test_data_y.data) | |
test_num += test_data_x.size(0) | |
test_acc = test_corrects.double().item() / test_num | |
print("测试的准确率为:", test_acc) |
# AlexNet 实战
class AlexNet(nn.Module): | |
def __init__(self, *args, **kwargs) -> None: | |
super().__init__(*args, **kwargs) | |
self.block = nn.Sequential( | |
nn.Conv2d(in_channels=1, out_channels=96, kernel_size=11, stride=4), | |
nn.ReLU(), | |
nn.MaxPool2d(kernel_size=3, stride=2), | |
nn.Conv2d(in_channels=96, out_channels=256, kernel_size=5, stride=1, padding=2), | |
nn.ReLU(), | |
nn.MaxPool2d(kernel_size=3, stride=2), | |
nn.Conv2d(in_channels=256, out_channels=384, kernel_size=3, stride=1, padding=1), | |
nn.ReLU(), | |
nn.Conv2d(in_channels=384, out_channels=384, kernel_size=3, stride=1, padding=1), | |
nn.ReLU(), | |
nn.Conv2d(in_channels=384, out_channels=256, kernel_size=3, stride=1, padding=1), | |
nn.ReLU(), | |
nn.MaxPool2d(kernel_size=3, stride=2), | |
nn.Flatten(), | |
nn.Linear(256 * 5 * 5, 4096), | |
nn.ReLU(), | |
nn.Dropout(0.5), | |
nn.Linear(4096, 4096), | |
nn.ReLU(), | |
nn.Dropout(0.5), | |
nn.Linear(4096, 10) | |
) | |
def forward(self, x): | |
x = self.block(x) | |
return x |
此处并不是标准是 AlexNet 模型,主要是为了适配 FashionMNIST。
train_process = train_model_process(AlexNet(), train_dataloader, val_dataloader, num_epochs=5) | |
matplot_acc_loss(train_process) |
由于主包的 GPU 实在是太慢了,就不放结果图了。
# VGG 网络原理
VGGNet 有 6 种不同的结构,主要以 VGG-16 为核心拆解。
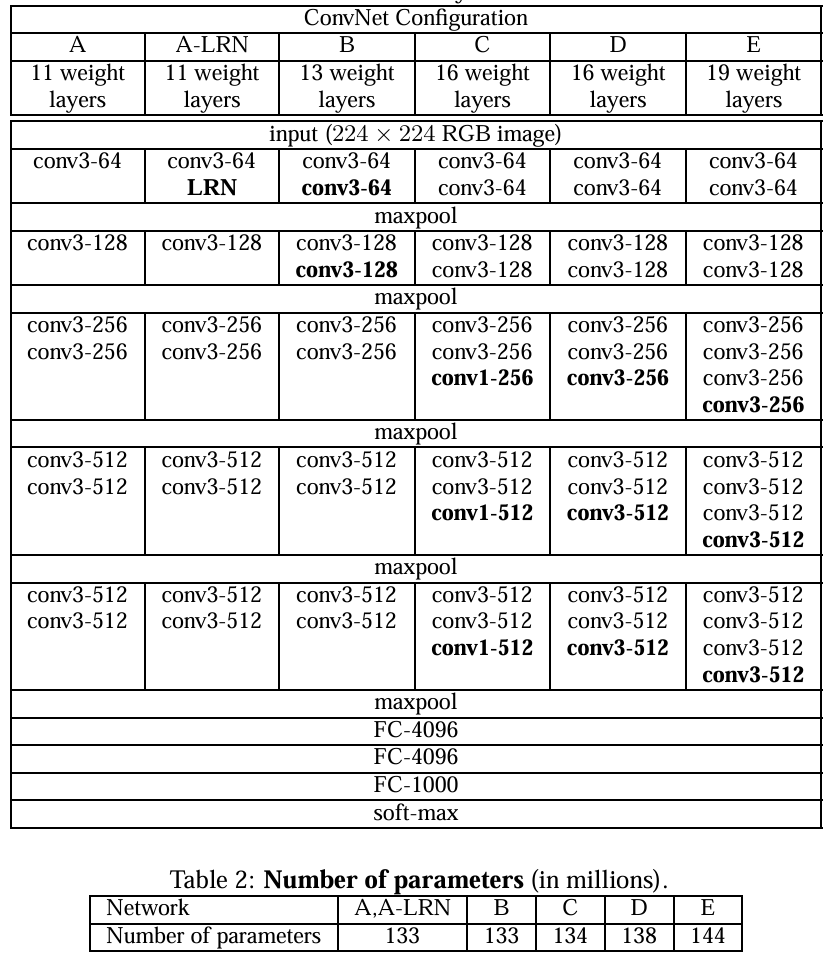
vgg-block 内的卷积层都是同结构的,池化层都得上一层的卷积层特征缩减一半,深度较深,参数量够大,较小的 filter size/kernel size
VGG 大量使用了 3 x 3 的卷积核,参数很小而且效果还不错。
还有 VGG 使用了块状结构,相当于一个小单元,非常方便。
# 模型
class VGG16(nn.Module): | |
def __init__(self): | |
super(VGG16, self).__init__() | |
self.block1 = nn.Sequential( | |
nn.Conv2d(1, 64, kernel_size=3, padding=1), | |
nn.ReLU(), | |
nn.Conv2d(64, 64, kernel_size=3, padding=1), | |
nn.ReLU(), | |
nn.MaxPool2d(kernel_size=2, stride=2) | |
) | |
self.block2 = nn.Sequential( | |
nn.Conv2d(64, 128, kernel_size=3, padding=1), | |
nn.ReLU(), | |
nn.Conv2d(128, 128, kernel_size=3, padding=1), | |
nn.ReLU(), | |
nn.MaxPool2d(kernel_size=2, stride=2) | |
) | |
self.block3 = nn.Sequential( | |
nn.Conv2d(128, 256, kernel_size=3, padding=1), | |
nn.ReLU(), | |
nn.Conv2d(256, 256, kernel_size=3, padding=1), | |
nn.ReLU(), | |
nn.Conv2d(256, 256, kernel_size=3, padding=1), | |
nn.ReLU(), | |
nn.MaxPool2d(kernel_size=2, stride=2) | |
) | |
self.block4 = nn.Sequential( | |
nn.Conv2d(256, 512, kernel_size=3, padding=1), | |
nn.ReLU(), | |
nn.Conv2d(512, 512, kernel_size=3, padding=1), | |
nn.ReLU(), | |
nn.Conv2d(512, 512, kernel_size=3, padding=1), | |
nn.ReLU(), | |
nn.MaxPool2d(kernel_size=2, stride=2) | |
) | |
self.block5 = nn.Sequential( | |
nn.Conv2d(512, 512, kernel_size=3, padding=1), | |
nn.ReLU(), | |
nn.Conv2d(512, 512, kernel_size=3, padding=1), | |
nn.ReLU(), | |
nn.Conv2d(512, 512, kernel_size=3, padding=1), | |
nn.ReLU(), | |
nn.MaxPool2d(kernel_size=2, stride=2) | |
) | |
self.block6 = nn.Sequential( | |
nn.Flatten(), | |
nn.Linear(512 * 7 * 7, 4096), | |
nn.ReLU(), | |
nn.Linear(4096, 4096), | |
nn.ReLU(), | |
nn.Linear(4096, 10) | |
) | |
def forward(self, x): | |
x = self.block1(x) | |
x = self.block2(x) | |
x = self.block3(x) | |
x = self.block4(x) | |
x = self.block5(x) | |
x = self.block6(x) | |
return x |
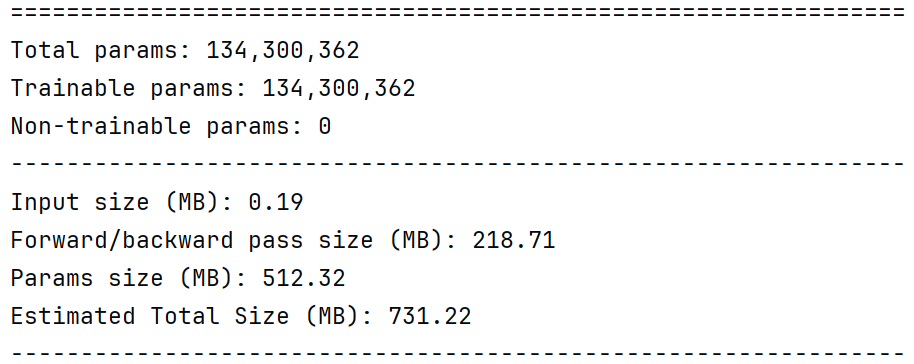
# 最佳实践 —— 权重初始化
在我们训练的时候,我们的模型可能不收敛,训练出来的结果图很难看,实际上大概率可能是出现了梯度消失问题,核心原因是我们的权重初始化过于随机了。
为什么权重初始化如此重要?
在深度神经网络中,权重初始化直接影响:
- 激活值的分布(前向传播)
- 梯度的大小和稳定性(反向传播)
- 模型是否收敛、收敛速度、最终性能
如果权重初始化不当,比如:
- 权重太小 → 激活值趋近于 0 → 梯度消失
- 权重太大 → 激活值饱和 → 梯度爆炸
所以我们必须要引入权重初始化!
# 何凯明 - 凯明初始化法
凯明初始化法(Kaiming Initialization),又称 He 初始化,由 何恺明(Kaiming He) 在 2015 年提出,专为 ReLU 及其变种(如 LeakyReLU) 设计的权重初始化方法。
for param in self.modules(): | |
if isinstance(param, nn.Conv2d): | |
nn.init.kaiming_normal_(param.weight, nonlinearity='relu') | |
if param.bias is not None: | |
nn.init.constant_(param.bias, 0) |
for param in self.modules(): | |
# 卷积层初始化 | |
if isinstance(param, nn.Conv2d): | |
nn.init.kaiming_normal_(param.weight, nonlinearity='relu') | |
if param.bias is not None: | |
nn.init.constant_(param.bias, 0) | |
# 全连接层初始化 | |
elif isinstance(param, nn.Linear): | |
nn.init.normal_(param.weight, 0, 0.01) | |
if param.bias is not None: | |
nn.init.constant_(param.bias, 0) |
以上可以放在:
class VGG16_init(nn.Module): | |
def __init__(self): | |
super(VGG16, self).__init__() |
初始化函数之下。
# 最佳实践 —— 调整批次
在深度学习中,调整批次大小(Batch Size) 是最有效、最低成本的性能调优手段之一。“最佳实践” 不是越大越好,也不是越小越精,而是根据硬件、任务、训练阶段动态权衡。
# GoogLeNet 网络原理
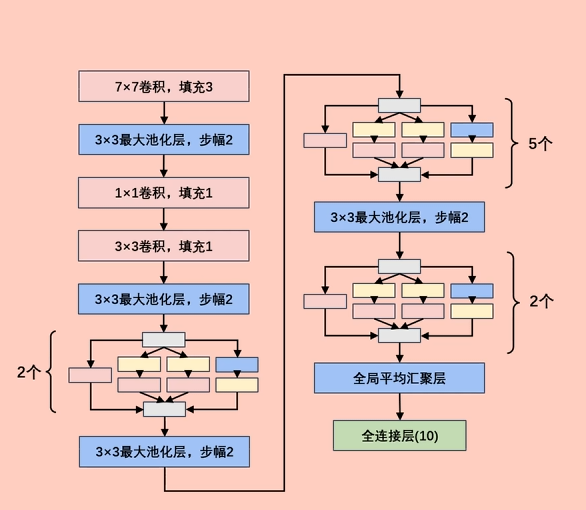
这里面最唬人的地方就是这个 Inception 块,实际上没有那么吓人。
以前流行的网络使用小到 1×1,大到 7×7 的卷积核。 本文的一个观点:有时使用不同大小的卷积核组合是有利的。
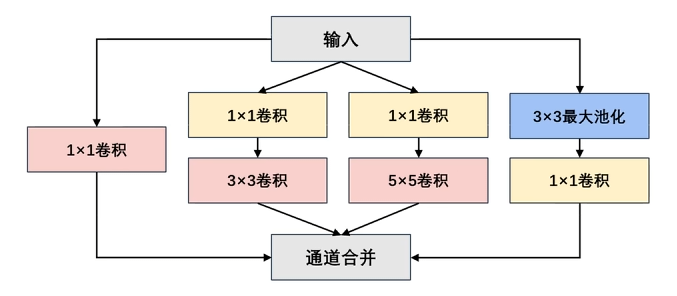
通道合并 :将四个路线输出的通道合并。
# 1 x 1 卷积的优点
** 在不改变空间结构的前提下,高效地融合通道信息、调整通道维度、引入非线性,从而提升模型表达能力并降低计算成本。** 实现跨通道的交互和信息整合,卷积核通道数的降维和升维,减少网络参数。
# 全局平均池化 GAP
优点:“无参降维 + 抗过拟合”—— 把特征图全局平均成单个数值,直接当分类 logits,省掉全连接层,大幅减少参数量且强制保留通道级语义,降低过拟合风险。
缺点:“丢细节 + 强假设”—— 空间信息被压成一点,对细粒度特征或目标定位任务无能为力,并隐含 “通道即类别” 的假设,若类别间特征重叠则易混淆。
注意区别:全局平均池化 GAP 与直接 Flatten 平展的区别
# 如何训练自己的数据集
在深度学习中,设计一个良好的模型需要基础知识与运气,在此基础之上,数据的预处理往往是拉开差距的关键点。
# 数据集的划分
如何将这样的数据目录:
data_cat_dog | |
├── cat | |
└── dog |
变成:
data | |
├── train | |
│ ├── cat | |
│ └── dog | |
└── test | |
├── cat | |
└── dog |
有这样的脚本:
import os | |
from shutil import copy | |
import random | |
def mkfile(file): | |
if not os.path.exists(file): | |
os.makedirs(file) | |
# 获取 data 文件夹下所有文件夹名(即需要分类的类名) | |
file_path = 'data_cat_dog' | |
flower_class = [cla for cla in os.listdir(file_path)] | |
# 创建 训练集 train 文件夹,并由类名在其目录下创建 5 个子目录 | |
mkfile('data/train') | |
for cla in flower_class: | |
mkfile('data/train/' + cla) | |
# 创建 验证集 val 文件夹,并由类名在其目录下创建子目录 | |
mkfile('data/test') | |
for cla in flower_class: | |
mkfile('data/test/' + cla) | |
# 划分比例,训练集:测试集 = 9 : 1 | |
split_rate = 0.1 | |
# 遍历所有类别的全部图像并按比例分成训练集和验证集 | |
for cla in flower_class: | |
cla_path = file_path + '/' + cla + '/' # 某一类别的子目录 | |
images = os.listdir(cla_path) # iamges 列表存储了该目录下所有图像的名称 | |
num = len(images) | |
eval_index = random.sample(images, k=int(num * split_rate)) # 从 images 列表中随机抽取 k 个图像名称 | |
for index, image in enumerate(images): | |
# eval_index 中保存验证集 val 的图像名称 | |
if image in eval_index: | |
image_path = cla_path + image | |
new_path = 'data/test/' + cla | |
copy(image_path, new_path) # 将选中的图像复制到新路径 | |
# 其余的图像保存在训练集 train 中 | |
else: | |
image_path = cla_path + image | |
new_path = 'data/train/' + cla | |
copy(image_path, new_path) | |
print("\r[{}] processing [{}/{}]".format(cla, index + 1, num), end="") # processing bar | |
print() | |
print("processing done!") |
# 数据的预处理
# 重调整
transforms.Resize(160) |
或
transforms.Resize((160,160)) |
第一个是的比例裁剪,第二个是指定像素裁剪,他们都是重调整。
# 随机裁剪
transforms.RandomResizedCrop(128, scale=(0.8, 1.0)) |
先随机在原图里裁出一块面积占 80 %–100 % 的区域,再直接 resize 成 128×128,既做了随机裁剪又做了尺度增强。
# 原始数据增强
transforms.AutoAugment(transforms.AutoAugmentPolicy.IMAGENET), |
自动从 ImageNet 预训练好的 25 种增强策略里,随机挑一条子策略(含 5 种强度可变的图像变换)作用到输入图上,属于 “自动数据增强” 里的经典算法,无需手工设计组合。
- 策略搜索阶段用强化学习在 ImageNet 上离线搜出 25 条子策略(每条含 5 个变换)。
- 每次训练迭代时:
- 随机选一条子策略;
- 按该子策略里指定的概率、幅度依次对图像做 5 次变换;
- 变换列表包括
ShearX/Y,TranslateX/Y,Rotate,Color,Posterize,Solarize,Contrast,Sharpness,Brightness,AutoContrast,Equalize等。
# 标准化
transforms.ToTensor() |
本身就具有归一化的功能,他将数值转化为 0-1 的区间,但这只是 “线性缩放”,不是真正意义上的 “标准化 (normalization)”。
transforms.Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225]) |
这才是真正的标准化:把数值变成均值为 0、方差为 1 的分布,加速模型收敛。
怎么算呢?还是来一个预处理。
from PIL import Image | |
import os | |
import numpy as np | |
# 文件夹路径,包含所有图片文件 | |
folder_path = 'data_cat_dog' | |
# 初始化累积变量 | |
total_pixels = 0 | |
sum_normalized_pixel_values = np.zeros(3) # 如果是 RGB 图像,需要三个通道的均值和方差 | |
# 遍历文件夹中的图片文件 | |
for root, dirs, files in os.walk(folder_path): | |
for filename in files: | |
if filename.endswith(('.jpg', '.jpeg', '.png', '.bmp')): | |
image_path = os.path.join(root, filename) | |
image = Image.open(image_path) | |
image_array = np.array(image) | |
# 归一化像素值到 0-1 之间 | |
normalized_image_array = image_array / 255.0 | |
# 累积归一化后的像素值和像素数量 | |
total_pixels += normalized_image_array.size | |
sum_normalized_pixel_values += np.sum(normalized_image_array, axis=(0, 1)) | |
# 计算均值和方差 | |
mean = sum_normalized_pixel_values / total_pixels | |
sum_squared_diff = np.zeros(3) | |
for root, dirs, files in os.walk(folder_path): | |
for filename in files: | |
if filename.endswith(('.jpg', '.jpeg', '.png', '.bmp')): | |
image_path = os.path.join(root, filename) | |
image = Image.open(image_path) | |
image_array = np.array(image) | |
# 归一化像素值到 0-1 之间 | |
normalized_image_array = image_array / 255.0 | |
try: | |
diff = (normalized_image_array - mean) ** 2 | |
sum_squared_diff += np.sum(diff, axis=(0, 1)) | |
except: | |
print(f"捕获到自定义异常") | |
variance = sum_squared_diff / total_pixels | |
print("Mean:", mean) | |
print("Variance:", variance) |
# 随机擦除
transforms.RandomErasing(p=0.3, scale=(0.02, 0.2)) |
以 30 % 的概率在图像上随机挖掉一块矩形区域(面积占图 2 %–20 %),用随机值(灰色、白色或黑色)填平,迫使模型学会 “靠局部也能猜对”,属于简单的正则化 / 抗遮挡增强。
# ResNet 原理与实战
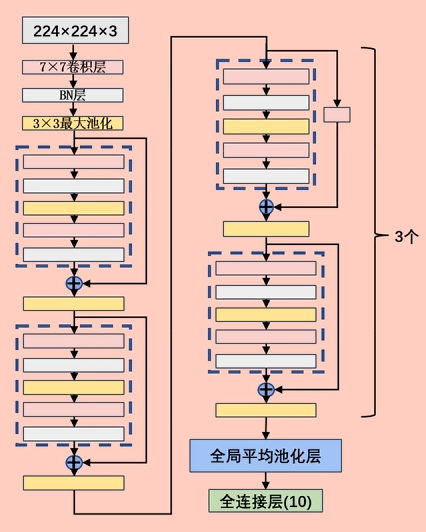
# 网络持续加深带来那些问题
一、优化难题:网络越深越 “学不动”
二、表达难题:网络越深越 “记不住”
三、工程难题:网络越深越 “养不起”
“深” 本身不是错,错的是深 + Plain 堆叠;,
Plain Network = 只有 “卷积–BN–ReLU” 一路串行下去,不带任何跳跃连接的直筒式架构。
“链式求导” 本身就是根源 —— 但要把话拆成两句说:
- 链式求导必然导致深度网络里的梯度是 “连乘” 形式;
- 连乘的因子一旦持续小于 1(或大于 1),层数一多就指数级衰减 / 爆炸,这就是梯度消失 / 爆炸的数学本质。
所以 Plain Net 的退化问题虽然表现形式是 “越深层训练误差越大”,但底层机制仍然绕不开链式求导带来的数值不稳定。
ResNet 的 skip connection 正是人为在链式乘积里插进一项 1,把 “连乘” 改写成 “连乘 + 1”,从而打断指数衰减 —— 用加法给链式法则打了一个补丁。
# 残差块
ResNet(Residual Network)的核心创新就是残差连接(Residual Connection),它解决了深层网络的梯度消失问题,使得训练非常深的网络成为可能。
残差块的设计是深度学习领域的重大突破,它不仅在图像识别任务中表现出色,还被广泛应用于各种深度学习架构中。a = h (x) + x
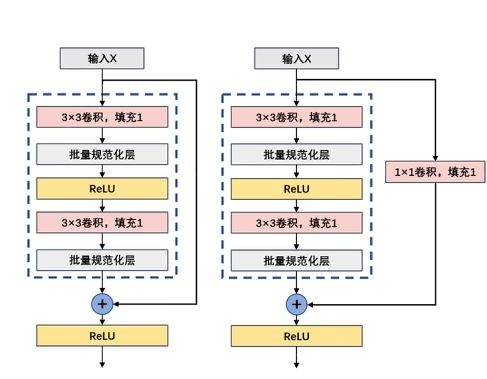
上图有一个错误,填充应该是 0,步幅是 1。
# Batch Normalization 归一化
Batch Normalization(批归一化,简称 BN) 的目的是 让神经网络训练更快、更稳定、更容易收敛。

BatchNorm 不是 “锦上添花”,而是 “深度网络能训得动” 的刚需 —— 它把每层的输入分布强行拉回 N (0,1),切断梯度消失 / 爆炸与内部协变量偏移的恶性循环,让链式求导的连乘因子始终落在 1 附近,于是非常深的 Plain/ResNet 才吃得下大学习率、快速收敛且不用特别精调初始化。
BN 的解决方案非常直观有力:既然层输入的分布老在变,那我们就强制把它拉回一个稳定、标准的分布。
BN 的位置通常放在:
全连接层/卷积层 → BatchNorm → 激活函数(ReLU等) |
# ResNet 的基本实现
# 残差块
class ResidualBlock(nn.Module): | |
def __init__(self, in_channels, out_channels, use_conv1x1=False, stride=1) -> None: | |
super(ResidualBlock).__init__() | |
self.RelU = nn.ReLU(inplace=True) | |
self.conv1 = nn.Conv2d(in_channels=in_channels, out_channels=out_channels, kernel_size=3, stride=stride, | |
padding=1) | |
self.conv2 = nn.Conv2d(in_channels=out_channels, out_channels=out_channels, kernel_size=3, stride=stride, | |
padding=1) | |
self.BN1 = nn.BatchNorm2d(out_channels) | |
self.BN2 = nn.BatchNorm2d(out_channels) | |
if use_conv1x1: | |
self.conv3 = nn.Conv2d(in_channels=in_channels, out_channels=out_channels, kernel_size=stride, | |
stride=stride, padding=0) | |
else: | |
self.conv3 = None | |
def forward(self, x): | |
y = self.RelU(self.BN1(self.conv1(x))) | |
y = self.BN2(self.conv2(y)) | |
if self.conv3 is not None: | |
x = self.conv3(x) | |
y = self.RelU(y + x) | |
return y |
# ResNet18
class ResNet18(nn.Module): | |
def __init__(self, ResidualBlock) -> None: | |
super(ResNet18, self).__init__() | |
self.b1 = nn.Sequential( | |
nn.Conv2d(in_channels=1, out_channels=64, kernel_size=7, stride=2, padding=3), | |
nn.BatchNorm2d(64), | |
nn.ReLU(inplace=True), | |
nn.MaxPool2d(kernel_size=3, stride=2, padding=1) | |
) | |
self.b2 = nn.Sequential( | |
ResidualBlock(64, 64, use_conv1x1=False, stride=1), | |
ResidualBlock(64, 64, use_conv1x1=False, stride=1) | |
) | |
self.b3 = nn.Sequential( | |
ResidualBlock(64, 128, use_conv1x1=True, stride=2), | |
ResidualBlock(128, 128, use_conv1x1=False, stride=1) | |
) | |
self.b4 = nn.Sequential( | |
ResidualBlock(128, 256, use_conv1x1=True, stride=2), | |
ResidualBlock(256, 256, use_conv1x1=False, stride=1) | |
) | |
self.b5 = nn.Sequential( | |
ResidualBlock(256, 512, use_conv1x1=True, stride=2), | |
ResidualBlock(512, 512, use_conv1x1=False, stride=1) | |
) | |
self.b6 = nn.Sequential( | |
nn.AdaptiveAvgPool2d((1, 1)), | |
nn.Flatten(), | |
nn.Linear(512, 10) | |
) | |
def forward(self, x): | |
x = self.b1(x) | |
x = self.b2(x) | |
x = self.b3(x) | |
x = self.b4(x) | |
x = self.b5(x) | |
x = self.b6(x) | |
return x |

